Natural Resource Biometrics

Log Volume Estimation

Log volumes can be estimated in a number of ways. Most methods estimate different portions of the log volume using different formulas.  Figure 1 below indicates the most commonly used formula for each portion of a tree.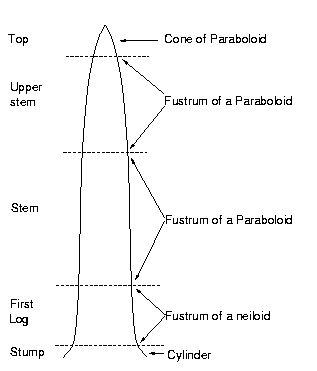

Each of these sections of the stem can be estimated using one of four basic equations;

Figure 2. The formula for the area of a cylinder.  
• Cylinder - The cylinder formula is the simplest of the formulas.  It requires only the area of one end and the length of the cylinder (see Figure 2).

• Cone - The cone is a tapered shape with a smaller upper area than the cylinder described above. The sides are a simple linear interpolation between the two ends (see Figure 3).

• Paraboloid - The paraboloid is a tapered shape that bows outward increasing the volume of the shape (see Figure 4). This shape has been traditionally recommended for determining the cubic volume of of logs. My opinion is that it is well suited to longer log lengths but may over estimate volume in short logs.

• Neiloid - The neloid is a tapered shape that bows inward decreasing the volume of the shape (see Figure 5). This shape is usually used for the stem between the stump and breast height (4.5 ft or 1.3 m). This shape works very well at describing this part of the tree stem.

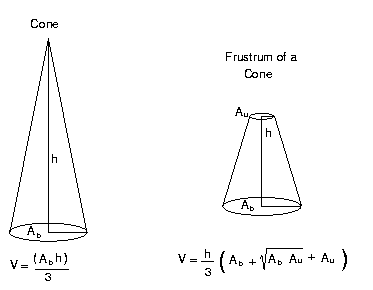
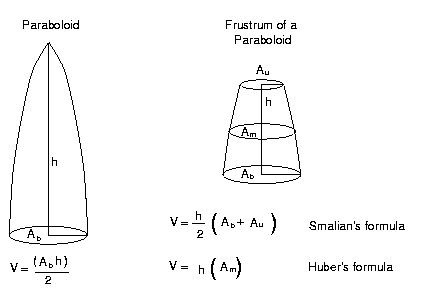
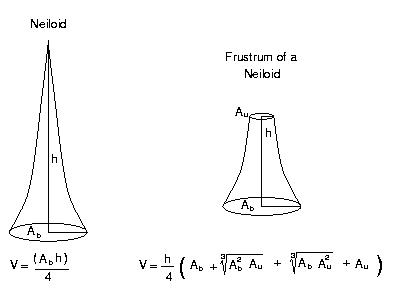
For the same input data these volumes will order this way:

1. the Cylinder will produce the largest volume as there is no taper,
2. the Paraboloid will be next in volume,
3. then the Cone is the middle of the tapered shapes, and
4. the Neloid is the least volume of all these shapes.

Diagram Log Rules

Diagram Rules are volume rules that depend on a saw pattern and assumed kerf (width between the boards, see Figure 6).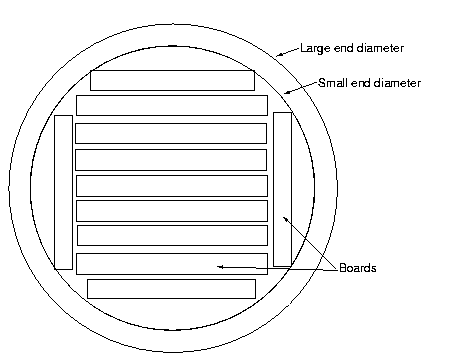

The most common diagram rule is the Scribner log rule.  The Scribner was proposed by J. M. Scribner and first published in 1846 (Husch et al. 1993).  It assumes a 1/4 inch kerf and 1 inch boards probably not less that 8 inches wide. (Chapman and Meyer, 1949).  The Scribner log rules are for logs with small end diameters from 12 to 44 inches and 10 to 24 feet in length.

Bruce and Schumacher (1950) fit a regression equation to the original table an produce the following equation:

V is volume in board feet,
D is small end diameter in inches,
L is log length in feet.
 

High overrun on logs less than 14 inches ( as high as 30 %).
overrun decreases up to 28 inches where is flattens out at about 3- 5 %.

Doyle Log Rule

This is one of the most widely use and well as one of the oldest log rules.  The rule was developed by Edward Doyle in 1825.   The rule states:

"Deduct 4 inches from the diameter of the log, D, in inches, for slabing, square  one-quarter of the remainder, and multiply by the length of the log, L, in feet."

This equivalent to squaring the log into a cant and calculating the board feet in the cant.  Doyle assumed 25 % reduction for kerf and shrinkage.  The rule can be stated as:

V is volume in board feet,
D is small end diameter in inches,
L is log length in feet.
 

The formula is very simple.
The rule works best for logs between 26 and 36 inches in diameter;
Larger logs produce underruns,
Smaller logs produce high overruns.

International log rule

One of the most accurate mathematical log rules was proposed by J. F. Clark (1906).  The log rule was developed for 4 foot sections of a log.   It assumes a 1/8 inch kerf and a 1/16 inch shrinkage.  Clark suggested a 1/2 inch taper per 4-foot section of log and so came up with the following formulas:

Clark suggest that logs larger that 20 feet be measured as multiples of one of these log lengths.

Also See:

Chapman, H. H. and W. H. Meyer. 1949. Forest Mensuration. McGraw-Hill Book Co. New York. 522 pp.,/p>

Clark, J. F. 1906. Measurement of Sawlogs.Forestry Quart. 4:79-93.

Chapter 8 in :

Husch, B., T. W. Beers and J. A. Kershaw. 2003. Forest Mensuration. Fourth Edition. John Wiley and Son 443 p.