Simple Linear Regression

Simple linear regression is a tool for fitting a linear line to a set of data.  It is used when you want to predict the value of the "dependent variable" Y by knowing the value of the "independent variable" X.

.

Figure 1 is an example of a data set with a regression line fit.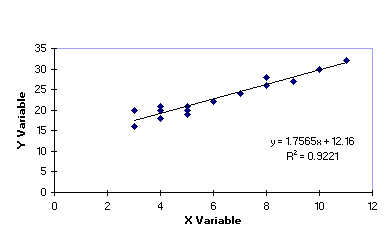

regression graph

Figure 1. Example data set with regression line fit to data.

The line in the graph can be described as:

$$ y = b_0 + b_1 x $$

where y is the dependent variable (also plotted on the y axis of the graph), x is the independent variable (plotted on the x axis of the graph). The parameters that are estimated are b0 and b1. 

These parameters can be estimated using the following equations:

$$ b_1 = \frac{\displaystyle\sum\limits_{i=1}^{n} x_i y_i - \frac{\left( \displaystyle\sum\limits_{i=1}^{n} x_i \right) \left( \displaystyle\sum\limits_{i=1}^{n} y_i \right) }{n}}{ \displaystyle\sum\limits_{i=1}^{n} x^2_i - \frac{\left( \displaystyle\sum\limits_{i=1}^{n} x_i \right)^2}{n}} $$


$$ b_0 = \bar{y} - b_1 \bar{x} $$

where Xi and Yi are the individual observation and n is the number of observations.

The results of a regression are often summarized using an analysis of variance table.
The usual configuration for the table is as follows:

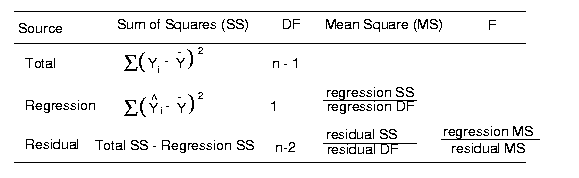regression anova

The F test is a test to determine if the regression explains more of the variation than the mean.  Another statistic that is commonly used to describe a regression is the coefficient of determination R2 This statistic is the proportion of the observed data explained by the regression.  This statistic is a value that ranges from 0 to 1 with 0 being no agreement between the regression and the data and 1 being perfect agreement between the data and the regression.

$$ R^2 = \frac{SS_{regression}}{SS_{total}} $$

Another important method of explaining  the results of a regression is to plot the residuals against the independent variable.  This analysis can be used to indicate that the model is mis-specified and  transformation required.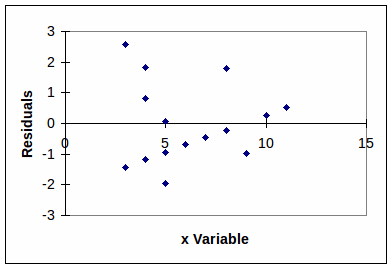

coefficient of determination

Figure 2. Residual plot of the data.


Also See:

Chapter 16 - Simple linear Regression pages 317-330 in:

Zar, J. H. 2007. Biostatistical Analysis. Prentice-Hall, Inc. Englewood Cliffs, New Jersey. 718 pp.
Creative Commons License
Natural Resources Biometrics by David R. Larsen is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License .

Author: Dr. David R. Larsen
Created: August 17, 1998
Last Updated: December 14, 2019