Cubic Log Volume
Cubic foot volume is calculated as the frustum of a geometric shape.
Frustum of a paraboloid or Smalain's Formula
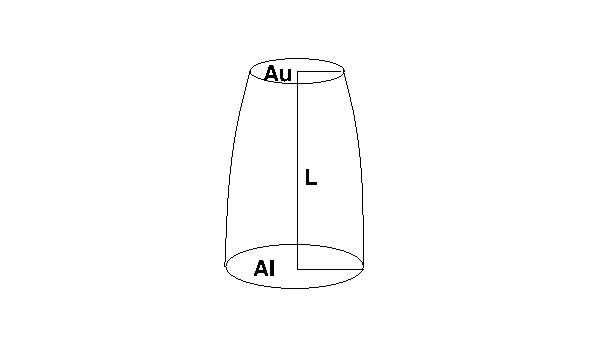
Figure 1. A frustum of a paraboloid or often call the Smalian's Formula.
$$V = \frac{L}{2} \left( As + Al \right)$$
where V is the cubic Volume in the dimensions of L3, As is the area of the small end in dimensions of L2, Al is the area of the large end in dimensions of L2. Note the diameter of the ends are ususally no measured in the same units as L so the units must be converted.
Frustum of a cone.

Figure 2. A frustum of a cone.
$$V = \frac{L}{3} \left( As + \sqrt{As Al} + Al \right)$$
where V is the cubic Volume in the dimensions of L3, As is the area of the small end in dimensions of L2, Al is the area of the large end in dimensions of L2. Note the diameter of the ends are ususally no measured in the same units as L so the units must be converted.
Frustum of a neiloid
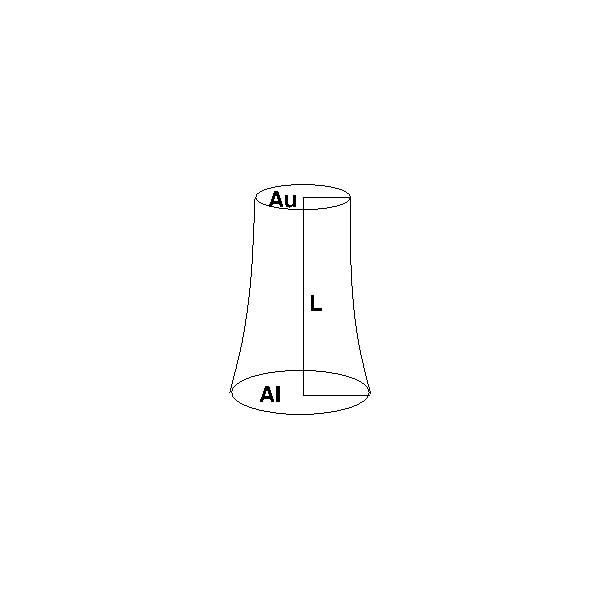
Figure 3. A frustum of a neiloid.
$$V = \frac{L}{4} \left( As + \sqrt[3]{As^2 Al} + \sqrt[3]{As Al^2} + Al \right)$$
where V is the cubic Volume in the dimensions of L3, As is the area of the small end in dimensions of L2, Al is the area of the large end in dimensions of L2. Note the diameter of the ends are ususally no measured in the same units as L so the units must be converted.
Example
- Imperial Units
- dia small = 10 in inches
- dia large = 12 in inches
- L = 16 feet
- unittype = "imperial"
- Answer (smalian) = 10.647 cubic feet
- Answer (cone) = 10.588 cubic feet
- Answer (neiloid) = 10.568 cubic feet
- Metric Units
- dia small = 25 in centimeters
- dia small = 29 in centimeters
- L = 5 in meters
- unittype = "metric"
- Answer (smalian) = 0.287848 cubic meters
- Answer (cone) = 0.286801 cubic meters
- Answer (neiloid) = 0.286452 cubic meters
Code
Excel® Visual Basic Code
R Statistical Package Code (Cone)
R Statistical Package Code (Smalian)
R Statistical Package Code (Neiloid)
Python Code (Cone)
Python Package Code (Smalian)
Python Code (Neiloid)
Go Code
C Code
|